The Ubiquitous and Seductive J Curve
March 14, 2008
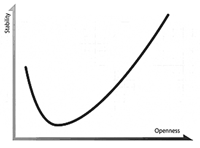
From The J Curve: A New Way to Understand Why Nations Rise and Fall.
Book Review
Philip J. Davis
The J Curve: A New Way to Understand Why Nations Rise and Fall. By Ian Bremmer, Simon and Schuster, New York, 2006 (hardcover), 320 pages, $26.00; 2007 (paperback), 336 pages, $11.00.
My doctor told me to keep a hot compress on my sore arm. But our cleaning lady told me to change it to a cold compress. She knew about the J curve.
---An old joke, updated
J curves are all over the map. They can be epitomized in the observation that more is sometimes also less and less is sometimes more. Eating is good for you, but too much stuffing can make you sick. Bells and whistles in a computer package can be useful, but too many of them can reduce user friendliness. Introduce (if you can) numerical measures of such "quantities," plot one against the other, and lo and behold, you will have produced a J curve (or perhaps an upside-down J). Easier still: Without quantization, label unscaled axes appropriately and draw a J curve freehand, and in this way produce a qualitative description of a certain phenomenon. Then, if you care to, draw predictions and policy conclusions---on, for example, the eruption of group violence.
Ian Bremmer has described the crises of the past hundred years or so as seen through a generic two-dimensional curve in the shape of a J that plots social stability against political and social openness. The linking of these qualities is by no means new. In my undergraduate days, Professor Roger Merri-man (a Roosevelt hater) said to us in the final lecture of his History I course:
"Gentlemen, the pendulum of history swings back and forth from liberty to security."
Same idea.
Did I say "generic"? Well, the Web site of the Eurasia Project* (Bremmer is president of the Eurasia Group) alludes to the shadow presence of some quantitative mathematics in J-curve analysis; such material has been suppressed and hidden from view in this book, presumably for the comfort of a targeted innumerate readership. For example: A "stability index" appears to be computed on the basis of twenty variables and is up-dated monthly. (If the combination is linear, did the coefficients drop from a platonic heaven or appear in a dream?) Such quantizations make possible a scaled plot and provide the cachet of objectivity to what is really subjective.
The J curve is not a constant of nature. As time goes by and as events unfold, Bremmer and his group push the curve up and down and massage it. "All states are in constant motion on the J curve," Bremmer writes, and that is how time, generally symbolized by mathematicians as t, gets into the act nonquantitatively. Irving Berlin's Depression-era song asserts that "Just around the corner, there's a rainbow in the sky" and that "Mr. Herbert Hoover says now's the time to buy," but the public was not told when the turnaround would occur, nor does the present sort of analysis inform us. Use of the pseudo-quantitative and pseudo-dynamic is a powerful ploy; wave some numbers around, and with a little bit o' luck you can convince the innumerate, and yourself as well.
I cannot go into the many geopolitical conclusions and strategies that Ian Bremmer, a political scientist, draws from his J curves. I certainly agree with some of them. Bremmer is a very smart cookie, a prolific author, and a sharp entrepreneur; the Eurasia Group (with appropriate disclaimers) serves as an adviser on political and economic risk for those whose fingers are on a variety of important buttons. Here are some simple statements relating to the minimum point of the J curve:
Descriptive: "Yugoslavia illustrates . . . that a state may fall into the depths of the J curve and fail to reemerge on either side."
Prescriptive: "Developed states should . . . work to create the conditions most favorable for a closed regime's safe passage through the least stable segment of the J curve.
Predictive: "It may not always be in the interests of the international community to push a relatively unstable left-side-of-the-curve into the transitional dip of the curve."
At the generic level, I react---not all negatively---to Bremmer's kind of methodology. I feel that it would be a good thing if politicians and other movers and shakers realized that the world is rarely linear or monotonic; it is not a world in which more is always more and less is always less (or the other way around). Of course, if the curve describing a phenomenon were sufficiently smooth, things would be locally monotonic and hence the policy of maintaining what's already in place would not be counterindicated.
I feel that it would be a good thing if theoreticians could refrain from reducing the world in all its manifestations to two dimensions (or even six or twelve).
As Hermann Hesse pointed out (Steppenwolf),
"Even the most spiritual and highly cultivated of men habitually see the world and themselves through the lenses of delusive formulas and artless simplifications."
Alas, reductionism, which was elevated to high status in Descartes' Discours de la m�thode (1637), is what we constantly invoke---and have to invoke---to enable our limited brains to deal with the complexities of the universe. Of course, with digital computers, able to handle hundreds, thousands of dimensions, draconic reduction is no longer necessary; yet despite myriads of complex computations, prediction science has a so-so batting average. (The last two hurricane seasons were much milder than predicted!)
It's not easy to fault a person who, on the basis of a theory he espouses, walks all the way to the bank. After all, isn't success in prediction the hallmark of the scientific method? No. Success in prediction is only one requirement (and some philosophers of science have contended that it shouldn't even be listed as a requirement). In its day, Ptolemy's planetary system was a good predictor. Newton's theories still reign supreme in many parts of applied mathematics, though its fundamentals have been trumped by Einstein. I've heard that even with some theories of quantum physics proved to umpteen decimal places, quantum theorists are still biting their nails.
Not wishing to feel intellectually naked in the presence of such back-of-the-book pluggers as Strobe Talbott (former deputy secretary of state) or Francis Fukayama (political economist) or Samuel A. DiPiazza, Jr. (global CEO at PricewaterhouseCoopers), I consulted an economist and a historian from my own roster of experts. The economist had serious questions about the implied regression analyses with twenty variables (not described explicitly in the book). And yet:
"The bottom line is that what Bremmer does is harmless but profitable for him. Anyone who uses his work for business decisions can cover his mistakes by saying that he was using state of the art techniques."
The historian, who years ago rejected Toynbee's "challenge and response" theory of the rise and fall of civilizations, and would hardly give the time of day to Oswald Spengler's older apocalyptic writings, said that historical generalizations are ipso facto suspect. Every case must be treated separately. As Heraclitus might have said: You cannot step into two identical civilizations.
***
I would place the methodology of this book in the category of qualitative analysis, considerably amplified by political/historical savvy, Monday-morning quarterbacking, and guesswork backed by intuition. The relative virtues of the quantitative and the qualitative have been discussed for some time. Throw a ball in the air: It rises, then it falls. This is a qualitative statement. Galileo gave us a quantitative description of the phenomenon. Both are useful, and an understanding of their respective domains of utility and their interplay is critical. An infant learns that if he/she pushes a dish of oatmeal off the high-chair tray, it will make a mess on the floor and papa/mama won't be happy. The quantitative invokes numbers; the qualitative calls in words, pictures, experiences, impressions, hunches.
According to some philosophers, quantity and quality are independent attributes. And once perceived, a quality cannot be reduced to more primitive concepts. Others see quality as depending on and subordinate to quantity. The qualitative often precedes the quantitative in time, and Lord Rutherford, Nobelist in physics, once remarked that "The qualitative is nothing but poor quantitative."
I seriously doubt that we could go to the moon relying solely on the qualitative. Dialectical materialists have emphasized the change in quality wrought by quantity and have made political hay with this aper�u. A look at the titles of articles in, say, the Journal of Qualitative Differential Equations reveals both quantity and quality to be useful and the two to be inextricably intermeshed.
The introduction of qualitative methods into mathematics is often attributed to Henri Poincar� in his topological consideration of the solutions of differential equations. At the very least, Poincar� gave the qualitative a terrific shot in the arm, promoting its usefulness when the quantitative is not available. Thinking largely in terms of representations by special functions,� Poincar� did not anticipate the existence of the electronic computers that now provide acceptable answers to complex systems of equations.
We desperately want to know the future. What actions shall we take now? How, over the millennia, has the future been revealed to us? In dreams, in the flight of birds, in the entrails of victims, in tarot cards, in the toss of a die, in the words of sacred texts, in the ambiguous prophecies of the possibly frenzied Pythia, in astrology (which in its golden period was deeply mathematical), in extrapolations from the past, in the differential equations of mathematical physics. . . . And we are willing to pay good money for someone who offers to invoke these methods and interpret what they reveal. Analysis by J curve now joins the long list of these (for the most part) still employed modalities. Given the vagaries of human nature and of the ambient world, the J curve might occasionally serve just as well as any of them.
*Check out the material on the stability of emerging markets.
�H. Poincar�, The Future of Mathematics, 4th International Congress of Mathematicians, 1908.
Philip J. Davis, professor emeritus of applied mathematics at Brown University, is an independent writer, scholar, and lecturer. He lives in Providence, Rhode Island, and can be reached at [email protected].

