ICIAM 2011: Mathematicians Gone Solar!
February 5, 2012
Fadil Santosa, director of the Institute for Mathematics and its Applications at the University of Minnesota, captures highlights of a four-part minisymposium, "Mathematical Sciences in Solar Energy Research," held at ICIAM 2011. He and Henry Warchall of the National Science Foundation's Division of Mathematical Sciences organized the sessions.
The amount of solar energy that reaches the earth in one hour is sufficient to supply the world's energy needs for one year. Harvesting this energy efficiently is a huge challenge. Most solar cells have low efficiency and are not very cost-effective. Other current solar energy technologies have drawbacks as well. There is a need for new technology that can capture the energy from the sun. To develop this technology, we need to understand what the challenges are and to engage a community of researchers who can devote their attention to this important problem.
We organized the four-part minisymposium to showcase cutting-edge mathematical research in solar energy. Our hope was that the sessions would strengthen the solar energy community by connecting researchers working in this field and by encouraging others to join them.
The idea for the session grew out of NSF's Solar Energy Initiative (SOLAR), which involves the Divisions of Chemistry, Materials Research, and Mathematical Sciences. SOLAR supports interdisciplinary efforts by groups of researchers to address the scientific challenges of highly efficient harvesting, conversion, and storage of solar energy. The intention of the program creators was to encourage new collaborations in which the mathematical sciences would be linked in a synergistic way with the chemical and materials sciences to develop novel, potentially transformative approaches in an area of much activity but largely incremental advances. What is somewhat unusual about this program is that each project must have three (or more) co-principal investigators, one each from chemistry, materials, and the mathematical sciences.
SOLAR was launched in 2008 and ended in 2011. To mobilize the mathematical sciences community, IMA organized the workshop Scientific Challenges in Solar Energy Conversion and Storage, which was held in November 2008. Seventeen projects were funded in FY 2009 and 2010; five additional projects were funded in FY 2011. Without this creative effort on the part of NSF, it is likely that few mathematicians would be working in this nationally important research area.
Believing that the time had come for an overview of solar energy research activities in which mathematical scientists are engaged, we invited the PIs from the 17 projects funded under the SOLAR program in FY 2009 and 2010 to participate in the minisymposium. Twelve of the 17 projects were represented.
The presentations fell roughly into two categories: materials modeling and process modeling. All the speakers discussed research related to photovoltaic solar cells, with one exception: Irene Gamba of UT Austin gave an interesting talk on a process that uses solar power to create hydrogen fuel (see Figure 1). This very complex photoelectrochemical process can be modeled by a system of partial differential equations. In addition to the huge potential impact of this work, it has already produced new and exciting mathematics. Analysis of the PDEs will require new techniques as these equations are very different from standard ones. Moreover, there is a need to develop computational techniques to solve these PDEs. 
Figure 1. Energy conversion strategies for light coming in and fuel going out come in three forms: natural biological photosynthesis in homogeneous chemistry (left), electricity in photovoltaics (right), and conversion of fluid into fuel by photoelectrochemistry (center). In photoelectrochemical experiments, irradiation of an electrode with light that is absorbed by the electrode material causes the production of a current (a photocurrent) that depends on wavelength, electrode potential, and solution composition and provides information about the nature of the photoprocess, its energetics, and its kinetics. Photoelectrochemical studies are frequently carried out to obtain a better understanding of the nature of electron transfer in semiconductor electrode/solution interfaces.
Models of photoelectrochemical processes for water splitting are simulated by semiconductor�electrolyte systems with a reacting flux transfer interface condition, involving the electron�hole pair redox reaction in the semiconductor�electrolyte system with a reacting flux transfer interface condition. These simulations are done under "dark" (only electron�hole recombinations) and "illuminated" (recombinations plus a photo generation term proportional to the absorption coefficient of the semiconductor and the corresponding surface photon flux). These simulations are based on a Gummel�Schwarz iteration algorithm for a drift�diffusion�Poisson system for the semiconductor region and a Poisson�Nernst�Planck system for the redox pair in the electrolyte region. From "On the modeling and simulation of semiconductor�electrolyte interfaces," Y. He, I.M. Gamba, A. Bard, H.C. Lee, and K. Ren, ICES, UT Austin, 2011.
Among the speakers on materials modeling was Hector Ceniceros of UC Santa Barbara, who described the modeling of materials needed in organic solar cells. The approach he advocated is based on field-theoretic models for polymeric fluids (see Figure 2). Keith Promislow of Michigan State discussed his work in modeling the microstructures in solid-state dye-sensitized solar cells. The phase-field method he developed is capable of capturing a range of microstructures that can emerge in these systems. (An article on Promislow's work appears in this issue.) Tobias Schneider of Harvard described a process for creating laser-doped silicon, which is a way to produce more efficient solar cells.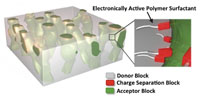

Figure 2. Designed electronically active interfacial materials for polymer-blend solar cells. Top, schematic of an all-polymer bulk heterojunction with a multifunctional, tri-block electroactive polymer surfactant additive. Bottom, due to limited exciton diffusion lengths in polymers, donor and acceptor must be dispersed in a bicontinuous morphology. Bicontinuous microemulsion morphologies are investigated via polymer field-theoretic models and simulations. Courtesy of project PIs Chabinyk, Ceniceros, Fredrickson, and Hawker.
Optics figure in a big way in solar cells. Boaz Ilan of UC Merced and Stephen McDowall of Western Washington University discussed the creation of devices that concentrate light using luminescent materials, modeled at the macroscopic level. At the microscopic level, photonic bandgap phenomena can be exploited to increase the efficiency of solar cells, the approach proposed in the talk of Christoph Kirsch of the University of North Carolina.
In a talk on modeling charge transport in a solar cell, Robert Krasny of the University of Michigan pointed out that a lot of basic processes need to be better understood and modeled before we can apply optimization tools to increase the efficiency of solar collectors.
Modeling at the electronic-excitation level is another important part of efforts to develop better and cheaper solar cells, as exemplified by the work of Zhaojun Bai of UC Davis and of John Lowengrub of UC Irvine.
As these sessions made clear, mathematicians are already making a difference in solar energy research. Their collaborative work has indicated new directions to explore, new experiments to conduct, and a better understanding of the fundamental phenomena at play. We are encouraged to see that the NSF investment in solar energy research is potentially transformative. It is not a stretch to predict that new mathematical research areas will emerge from these efforts. What a glorious and sunny opportunity for mathematics!
Readers can find a complete list of speakers in the four-part minisymposium by following the links at http://meetings.siam.org/sess/dsp_programsess.cfm?SESSIONCODE=12247.

