Atomistic-to-Continuum Coupling
September 24, 2006
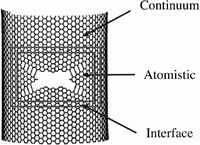
Figure 1. Illustration of an AtC carbon nanotube fracture simulation, with an atomistic domain surrounding the failure region and a continuum domain elsewhere. The domains are bridged by an interface, or �handshake,� region. Image courtesy of T. Belytschko [1].
Michael L. Parks and Richard B. Lehoucq
On March 20, 2006, researchers from around the world gathered in Albuquerque, New Mexico, for a two-day workshop on atomistic-to-continuum (AtC) coupling an-alysis. The Computer Science Research Institute at Sandia National Laboratories sponsored the workshop, which was organized by Claude Le Bris (Ecole Nationale des Ponts et Chauss�es), Jacob Fish (Rensselaer Polytechnic Institute), and Pavel Bochev, Rich Lehoucq, and Greg Wagner (Sandia National Laboratories).* The goal was to understand and quantify the limits in atomistic-to-continuum coupling and their impact on multiscale simulations.
Multiscale Processes: Modeling Challenges
Many important physical phenomena, such as deformation and failure, are inherently multiscale processes that cannot always be modeled via traditional finite element analysis. The finite element solution may be invalid if the scale of the domain is small enough to make the continuum approximation dubious, or if complex atomistic processes dominate the macroscopic behavior. In such situations modelers must resort to atomistic descriptions to resolve the underlying physics. Fully atomistic simulations of most domains of interest are not computationally feasible, however, and researchers must look to multiscale methods that couple atomistic and continuum simulations.
AtC coupling makes it possible to perform a continuum calculation over the majority of a domain of interest while limiting the more expensive atomistic simulation to a subset of the domain. Unfortunately, combining atomistic and continuum calculations is challenging: The former are based on individual nonlocal force interactions between atoms, while continuum calculations deal with bulk properties of matter that represent the averaged behavior of huge numbers of atoms. Consequently, methods must be coupled across length and time scales spanning many orders of magnitude---from the atomic to the macroscopic.
Applications have been a driving force in the development of AtC coupling methods. An understanding of the failure of carbon nanotubes (CNTs), for example, is essential to designers of CNT-reinforced composites. Accordingly, AtC simulations have been performed to model the physical properties and the effects of defects of CNTs. Because a fully atomistic simulation is not feasible in this case, atomistic representations are used in localized regions where individual atom positions are important, with a less expensive continuum representation used elsewhere, as shown in Figure 1. The two simulations are coupled through an interface, or "handshake," region.
Another important application is the modeling of material failure, which also requires understanding and modeling of nanoscale behavior. The material around a crack tip experiences large deformations, and the assumptions of linear elasticity break down in this region. Fracture models based on continuum mechanics theories, such as cohesive surface models, require a priori knowledge about the failure path, whereas atomistic simulations require no such information. In an AtC simulation, the region immediately surrounding the crack tip is modeled with atomistics (possibly including quantum mechanical principles), with a finite element model used for the remaining region. Coupling of atomistic and continuum simulations provides a computationally efficient mechanism for investigating not only the behavior of crack tips at a fundamental level, but also other phenomena, including grain boundaries and dislocations. Surveys of existing methods and techniques can be found in [5,8,12]; recent mathematical results are presented in [4].
Toward a Mathematical Theory for AtC Methods
Numerous AtC algorithms have been developed for specific applications, but much less effort has been directed to the mathematical theory of AtC methods. A rigorous mechanical formulation is lacking, as are error, stability, and convergence analysis, and uncertainty quantification for coupled atomistic and continuum models. A mathematical and mechanical framework that can provide a unified theoretical foundation for the formulation, analysis, and implementation of AtC coupling methods is an important open problem that served to focus the AtC workshop.
The workshop featured eight speakers, who addressed several fundamental issues with AtC coupling, including the pros and cons of existing AtC coupling methods, fundamental mechanical distinctions between atomistic and continuum models and their impact on coupling methods, and the physical relations that must hold for any valid coupling method. The workshop also provided a forum for informal discussions of participants' research.
The following summaries of the eight talks serve as an outline of the workshop themes:
- Considering both fluid and solid problems, Mark Robbins of Johns Hopkins University demonstrated a robust hybrid multiscale method that ties together continuum and atomistic domains across disparate length and time scales. In his framework, atomistic and continuum simulations are coupled through overlap regions in which the continuum region sets boundary conditions for the atomistic region and vice versa. Among other examples, Robbins presented highly accurate results for true bidirectional coupling between atomistic and continuum domains for dynamic Couette flow while correctly accounting for mass and heat flux [9].
- J. Tinsley Oden of the University of Texas provided succinct motivation for his talk: The path to error is also the path to truth. To arrive at the truth, we need only quantify the error and remove it. In any simulation, he said, we describe a physical event by a mathematical model, with the goal of calculating some quantity of interest. In general, the actual mathematical model we seek to solve is intractable, and so we replace it with a tractable surrogate model. This gives us (almost) the right answer for the surrogate model, but still the wrong answer for the true model.
- Oden introduced the idea of goal-oriented adaptive modeling [10], a general framework in which the surrogate model is adapted to reduce error (measured in terms of quantities of interest) to within a predetermined tolerance. As an example he considered the analysis of complex multiscale behavior encountered in the nano-manufacture of computer chips.
- Leonid Berlyand of Pennsylvania State University began with a discussion of continuum and discrete models of highly packed particle-filled composites. Starting from a continuum PDE model, he derived a discrete network approximation. This model, which can be thought of as a structural rather than a numerical discretization, provides physical understanding of the problem that cannot readily be extracted from the corresponding continuum model.
Berlyand then described a discrete mass�spring system, using the method of mesocharacteristics and the discrete Korn's inequality to develop sufficient conditions for the admission of a rigorous continuum limit for the network [2]. This result is applicable to nonperiodic arrays of particles, of which periodic arrays can be treated as a special case. - Fr�d�ric Legoll of Ecole Nationale des Ponts et Chauss�es gave a detailed analysis of a prototypical one-dimensional AtC coupling scheme [3]. Considering the case of a solid that deforms smoothly in some regions but not in others, Legoll pointed out that both atomistic and continuum models can be used and must be coupled. The efficacy of such a technique is dependent on the body force applied in the model. Additional difficulties arise if the interatomic potential model is not convex. Discretizing the continuum region with finite elements resolves some of these issues, essentially regularizing the model.
- Ron Miller of Carleton University opened his talk with a brief overview of the quasi-continuum (QC) method, which was developed for zero-temperature problems. He then discussed the extension of QC to finite-temperature simulations through a correction to the QC Hamiltonian. In an analogy to the ghost force correction used in zero-temperature QC, he called this correction a "ghost entropy" correction. Even with a quasi-harmonic approximation used to model the atomic motion, he showed several examples in which the resulting finite-temperature QC formulation reproduced the thermal expansion and temperature-dependent elastic constants of the underlying atomistic model with only modest error, even at high temperatures [6].
- Xiantao Li of Penn State presented his work with Weinan E of Princeton on appropriate boundary conditions for molecular dynamics simulations of crystalline solids [7]. A desirable MD boundary condition, he explained, prevents phonon reflection, maintains a correct temperature, and allows coupling with a continuum. An exact reflectionless MD boundary condition can be determined, but it is nonlocal in both space and time and its time�history kernel decays quite slowly. Accordingly, much research has gone into the search for less computationally expensive alternatives. Li demonstrated one such alternative, based on a variational approach, that closely reproduces the exact solution.
- In a joint talk, Eduard G. Karpov of Northwestern University and Dong Qian of the University of Cincinnati discussed the bridging-scale approach for AtC coupling. Unlike the many AtC methods that require refinement of a finite element mesh down to an atomic lattice, the bridging-scale method overlays an atomistic domain with a finite element mesh and projects the atomistic solution onto the mesh; in this way the approach avoids problems associated with extreme refinement of the finite element mesh. The speakers covered general AtC issues within the framework of the bridging-scale method, and also introduced the virtual atom cluster (VAC) model [11].
- In another joint presentation, Bob Haber and doctoral candidate Brent Kraczek of the University of Illinois at Urbana-Champaign discussed AtC coupling within a space�time discontinuous Galerkin (SDG) framework. After introducing SDG in a continuum and then in an atomistic setting, they turned to a discussion of how the two can be coupled. The SDG formulation effectively balances energy and momentum between the continuum and atomistic regions, they said, achieving highly accurate numerical results.
The workshop concluded with an open-floor discussion of current directions and open problems. In particular, participants observed that model validation will require closer interaction between mathematicians and physical scientists.
Slides from the eight presentations can be found on the conference Web site, www.cs.sandia.gov/CSRI/Workshops/2006/AtCCouplingMethods/. A special issue of the International Journal for Multiscale Computational Engineering (www.begellhouse.com/journals/61fd1b191cf7e96f.html) will publish papers on the workshop theme of AtC coupling analysis. In approximately a year, a second workshop, organized by J. Tinsley Oden, will be held at the University of Texas at Austin.
Acknowledgments
The authors acknowledge the helpful comments of P.B. Bochev and J. Fish.
References
[1] T. Belytschko, S.P. Xiao, G.C. Schatz, and R.S. Ruoff, Atomistic simulations of nanotube fracture, Phys. Rev. B, 65 (2002).
[2] M. Berezhnyy and L. Berlyand, Continuum limit for three-dimensional mass-spring networks and discrete Korn's inequality, J. Mech. Phys. Solids, 54 (2006), 635�669.
[3] X. Blanc, C.L. Bris, and F. Legoll, Analysis of a prototypical multiscale method coupling atomistic and continuum mechanics, Math. Model. Num. Anal., 39 (2005), 797�826.
[4] X. Blanc, C.L. Bris, and P.L. Lions, Atomistic to continuum limits for computational materials science; http://www.ann.jussieu.fr/publications/2005/R05048.pdf; submitted 2006.
[5] W. Curtin and R. Miller, Atomistic/continuum coupling methods in multi-scale materials modeling, Model. Simul. Mater. Sci. Eng., 11 (2003), R33�R68.
[6] L. Dupuy, E. Tadmor, R. Miller, and R. Phillips, Finite temperature quasicontinuum: Molecular dynamics simulations without all the atoms, Phys. Rev. Lett., 95 (2005), 060202.
[7] W. E and X. Li, Boundary conditions for molecular dynamics simulations of solids at low temperature, Comm. Com. Phys., 1 (2006), 136�176.
[8] J. Fish, Bridging the scales in nano engineering and science, J. Nanopart. Res., (2006), in press.
[9] X.B. Nie, S.Y. Chen, W.N. E, and M.O. Robbins, A continuum and molecular dynamics hybrid method for micro- and nano-fluid flow, J. Fluid Mech., 500 (2004), 55�64.
[10] J.T. Oden and K. Vemaganti, Estimation of local modeling error and goal-oriented adaptive modeling of heterogeneous materials, part I : Error estimates and adaptive algorithms, J. Comp. Physics, 164 (2000), 22�47.
[11] D. Qian and R. Gondhalekar, A virtual atom cluster approach to the mechanics of nanostructures, Internat. J. Multiscale Comp. Eng., 2 (2004), 277�289.
[12] D.D. Vvedensky, Multiscale modelling of nanostructures, J. Phys. Condens. Matter, 16 (2004), R1537�R1576.
M.L. Parks is a postdoctoral fellow at Sandia National Laboratories, supervised by R.B. Lehoucq and P.B. Bochev. Details about his work and research interests, which include multiscale analysis, iterative methods, domain decomposition, and numerical linear algebra, can be found at http://www.cs.sandia.gov/~mlparks/. R.B. Lehoucq is a member of the technical staff at Sandia National Laboratories.
*In January 2005, the Advanced Scientific Computing Research (ASCR) office of the U.S. Department of Energy's Office of Science solicited proposals for multiscale mathematics research and education. The program, Atomic to Macroscopic Mathematics, was established to develop a deeper understanding of the mathematics of physical phenomena at multiple length and time scales, and their interactions. Further information can be found in the RFP at www.science.doe.gov/grants/FAPN05-16.html. The workshop described here and Sandia's AtC initiative are funded under this program.

