Self-Organization of Complex Biological Phenomena
September 24, 2007

Figure 1. A pair of bacteria (highlighted, center), swimming from right to left, is initially misaligned and on a collision course (a). After an initial approach and a brief interaction (b), the bacteria become aligned, parallel to one another (c). They will remain parallel as they continue to swim---an instance of irreversible alignment of active particles.
Dmitry Karpeev
Late in April, about two dozen researchers from the United States and Europe met at Argonne National Laboratory for a three-day workshop, Multiscale Modeling of Self-Organization in Active Biological Systems. The workshop was motivated by recent strides in multiscale analysis, coupled with new results in the modeling of complex biological systems. The time seemed right, says Igor Aronson, one of the organizers, to bring together researchers in applied mathematics, physics, and biology---disciplines once considered distinct---to review recent developments and to compare models that promise new insights into the self-organization of complex biological systems.
Self-organization is the process whereby the internal structure of a system spontaneously increases in complexity even as stable spatiotemporal patterns develop. Energy is dissipated in this process, during which the system is thermodynamically open and far from equilibrium. Some of the early work on self-organizing systems focused on physical processes; in particular, physicists investigated pattern formation and evolution in granular materials agitated (e.g., shaken) by an external mechanism. Results of that research are now being applied to studies of other "active" systems---biological, chemical, and even social systems. The agitating mechanisms are internal to the systems, but they must consume energy and matter to keep the mechanisms running.
The two dozen presentations at the workshop clearly demonstrated the wide range of systems being studied. Among the topics discussed were the rheology and dynamics of cytoskeletal protein networks, instabilities in ensembles of swimming bacteria, insulator�metal transition in ion channels, the flocking of birds, and the evolutionary emergence of multicellular organisms from colonies of unicellular individuals.
Experimentation
How do simple components organize themselves into large-scale structures? Several speakers described experiments designed to answer this question. In one such experiment, researchers studied the effects of actin filaments interconnected by stationary crosslinkers or immobilized molecular motors on filament networks stiffened by mobile molecular motors. Micro-flow experiments conducted to quantify and validate models of directional sensing revealed that some cells were able to detect chemical gradients with high precision.
Another study considered the possibility that flagella-generated fluid flows provide a driving force for evolutionary transitions to multicellularity. In a third study, a modified version of particle-imaging velocimetry was used to quantify spatial and temporal correlations of velocity and vorticity in systems of swimming bacteria; observations include greater velocity for groups of coherently swimming organisms than for individual swimmers, as well as apparently turbulent behavior, despite the low Reynolds number of the generated flow.
Concluding the first day of the workshop was a tour of Argonne's materials science lab. There, workshop participants were shown an experiment on bacterial populations that were incapable of detecting an electric field but were very sensitive to ionic environments. The bacteria were subjected to electrically controlled spatially varying pH levels in thin liquid films. A goal of the experiment was to study the effects of dynamic adjustments in bacterial density on large-scale flow correlation. Surprisingly, the researchers detected considerable in-creases in swimming velocity and sharp increases in flow correlation with increased bacterial density. Another important observation was the alignment of previously unaligned pairs of bacteria following hydrodynamic interactions in the presence of induced flows (Figure 1).
Theory and Modeling
Complementing the experimental work on self-organization were several presentations focusing on theory, modeling, and analysis. Studies of cylindrical self-propelled bacteria, for example, have produced new data about the appearance and decay of localized groups; this data, together with analysis of local energy balance and individual cell trajectories, has provided the basis for a rational theory of biofluid dynamics.
In two presentations, researchers described a detailed model that accounts for hydrodynamic interactions in suspensions of self-locomoting rods. An interesting prediction of the theory was the difference in the behavior of "pushers," propelled by a force applied behind the rod in the direction opposite their motion, and "pullers," applying the force ahead of themselves: The former tend to align, the latter to diverge.
Another study modeled the flocking behavior of birds by treating them as polar rods with a tendency to align with their immediate neighbors. The essential feature of most such theories is the coupling of the local motion to the order parameter describing the local phase. In this simple model, interesting behavior---including superdiffusion (i.e., a diffusion-type process with the mean square displacement increasing faster than the first power of time)---was observed, elucidating the essential dynamics of the real system. Superdiffusion is traditionally associated with the onset of large-scale coherent motion and slow decay of spatial and temporal correlations.
Several speakers discussed organisms that move by "treadmilling"---a process driven by polymerization and depolymerization (e.g., of tubulin monomers), occurring at the opposite ends of a biopolymer, such as a microtubule or an actin filament. The studies identified the basic instabilities responsible for the dynamics of the system, such as the decrease in monomer concentrations and the depletion of GTP proteins.
Simulation and Multiscale Studies
Simple models can capture surprisingly rich behavior and can be treated analytically. Most even moderately complicated systems, however, are amenable only to numerical simulation. Most of the conclusions about models presented at the workshop were derived from simulations of the model dynamics. In conjunction with the essential instabilities identified analytically, simulations provided deep insight into the self-organizing behavior of the modeled systems.
In many cases, describing a complex self-organizing system at an acceptable level of fidelity, while capturing the behavior of interest, seems to require a multiscale approach. The reason is that the essential dynamic mechanisms of self-organization reside at the microscopic level, whereas the observable behavior and patterns are manifested macroscopically. Recent experiments have shown, for example, that microtubules driven by molecular motors are capable of sustaining a wide variety of large-scale two-dimensional structures. Underlying this phenomenon is a multiscale process, with nonlinear interactions between polar rods on a microscopic scale resulting in the emergence of macroscopic asters, vortices, and bundles whose behavior is essential to the functioning of the cell.
By adopting a multiscale approach, researchers were able to identify an orientational instability in microtubules that was not accounted for in earlier models. Analysis of the model revealed the location and the structure of the phase boundary delineating domains with differing patterns, as well as the disordered phase.
Recent results of this study reveal the importance of "passive crosslinkers"---immobile motors that bind filaments together and act as pivots while mobile motors process the rods. The presence of crosslinkers leads to "filamentation"---a type of bundling characterized by alignment of the rods along the bundles (Figure 2b). For bundles formed at high motor densities, but without crosslinkers, the orientations of the rods and bundles are not correlated (Figure 2a).
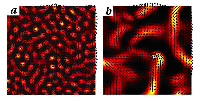
Figure 2. Composite image of density and orientation fields illustrating bundling instabilities in a mixture of biopolymers interacting via molecular motors and crosslinkers (simulation). Dark areas indicate low density, and bright areas, high density; the filament orientation field is shown by black arrows. Without crosslinkers (panel a), the density modulations are uncorrelated with filament orientation. With the crosslinkers (panel b), the filament orientation is predominantly along dense bundles.
Much of the study, including the results shown in Figure 2, was done by means of numerics and simulation, typical of modern studies of this type. Interestingly, another group of researchers used essentially the same model of alignment to describe the clustering dynamics of opinions---an application to social science of a theory that originated in physics and biology.
Microscopic Simulations
While large-scale patterns define the macroscopic scale of a model, the mechanics of the alignment of individual rods must be modeled at the microscopic scale. In particular, to understand the effects of flexibility in protein polymer filaments, researchers studied the interaction of pairs of rods, using a nonlinear elasticity model.
Figure 3 illustrates the effect of motors on soft filaments, such as actin, in a cell's skeleton. In this model a motor binds to a pair of filaments and moves along them with a constant velocity, resulting in a singular force acting on the rods. Above the critical motor velocity or, equivalently, above the critical solvent viscosity, this action results in the formation of multilooped structures in the filaments, which are representative of the buckling instability. These structures may affect the conformation of filaments in actin networks and may be responsible for the network rheology and the elastic behavior of the cell.
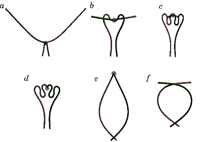
Figure 3. Simulation of a pair of actin filaments in a viscous environment; molecular motors cause the filaments to interact. Above the critical viscosity of the solvent, the filaments buckle, as predicted by the model.
New Insights
As evidenced by this workshop, the combined efforts of researchers in physics, materials science, biology, and computer science are yielding exciting new insights into self-organizational behavior in biological systems. And applied mathematics plays a key role, providing the tools needed for the description, analysis, and prediction of these active systems.
The workshop was organized by Igor Aronson, a materials scientist, and Dmitry Karpeev, a mathematician, both at Argonne National Laboratory, and Ray Goldstein, the Schlumberger Professor of Complex Physical Systems at Cambridge University. Funding was provided by the Office of Advanced Scientific Computing Research, U.S. Department of Energy. Further information about the workshop can be found on the conference Web site, http://www.mcs.anl.gov/dynamics/so07/.

