An Increasing Role for Mechanics in Cancer Modeling
October 21, 2007
Luigi Preziosi
A deep interest in cancer modeling among the research community has intensified in recent years. Evidence can be found in the numbers of talks at recent international meetings: The program for the most recent (2006) SIAM Conference on the Life Sciences included 30 tumor-related talks, about 8.5% of the total; at earlier meetings such communications could be counted on one hand, accounting for no more than 2 to 3% of the total. Similar trends have been observed by the Society for Mathematical Biology and the European Society for Mathematical and Theoretical Biology (ESMTB). In light of these developments, ESMTB and ICIAM agreed to embed a two-day meeting on computational cell biology in ICIAM '07. The ICIAM program itself also included twenty minisymposia on biomedical/biomathematical applications, four specifically on cancer modeling.
This surge of activity has led to rapid improvements in the way we approach cancer modeling. Traditional models described tumors as made up of only one type of cell and as having constant density. In the last few years, as it became evident that such descriptions were insufficient, our group, in collaboration with Helen Byrne, began to develop multiphase models [2]. The newer models account for the presence of several types of cells, e.g., tumor and host cells, living, replicating, and dying in a porous extracellular matrix, itself made up of several constituents, all bathed in a physiological extracellular fluid filled with proteins and growth factors that affect the behavior of the cells.
A further step forward has come with the growing realization that along with chemical signalling, mechanics plays an important role in tumor development. In fact, it has become common knowledge that a check-up is warranted on the discovery of any unusual growth--a mole or cyst, a nodule stiffer than the surrounding tissue, or any growth with a strange consistency. In other cases, the first indication of the presence of a tumor is reduced functionality of compressed neighboring tissue.
All this leads to several mechanics-related questions. How does a normal ensemble of cells know when to replicate and when to stop replicating? How can we evaluate the stresses and strains resulting from interactions of a tumor with surrounding tissues? How do the mechanical properties of a tissue change as the tumor grows? How do they influence cell behavior? For instance, results of some experiments [5] suggest that cell malignancy is influenced by the cells' environment. Stem cell differentiation is often determined by properties, both chemical and mechanical, of the substrate. Interest in all these questions explains the increasing attention of the biomedical community to mathematical and mechanical models of cell evolution and behavior.
Regarding the first question, a physiological mechanism called "contact inhibition of growth" comes into play: Cells do not duplicate if they sense that the space and environment available are inadequate; they are ready to re-activate their replication program, however, if conditions change--if, say, a neighboring cell dies. In [3] we showed how even the smallest failure in the mechano�transduction pathway can lead to a misperception of the compression state of local tissue and, thus, of the subsequent stress on a cell. This may represent a clonal advantage for a corrupted cell over its neighbors; it can lead to proliferative disorders, with the development of hyperplasia and, eventually, invasion and replacement of healthy tissue by the tumor. Jorg Galle [4] presented similar results in Zurich, at the ESMTB embedded meeting, using an individual cell-based model rather than a multiphase model.
During tumor growth, mechanical interactions between the tumor and surrounding tissues are of great importance. The pressure exerted by the external tissue influences cell duplication. In addition, the growing tumor, if encapsulated, will deform and chemically degrade the membrane, changing its mechanical properties and possibly causing it to rupture; this was the focus of the presentation by Olivier Saut [7] in the ICIAM '07 minisymposium "Tissue Defor-mation and Cell Motility: A New Frontier in Cancer Modeling." Finally, as mentioned earlier, pressure exerted by the tumor on surrounding tissues or capillaries can alter or compromise the functionality of the host tissue.
All this requires that we try to understand the mechanics of growing bodies--not an easy task and one in which fundamental mathematical questions arise: How can we describe the mechanical behavior of continuously remodeling tissues? It is not only tumor growth that needs to be considered. Tumor cells are bound to other cells and to the extracellular matrix by adhesion molecules of limited strength. Tumor growth and the resulting deformation thus generate continuous cell reorganization. On the basis of experimental evidence of these effects, we proposed [6] the existence of a threshold condition below which an ensemble of cells sticks to the extracellular matrix and moves with it; cells and extracellular matrix can deform, but adhesion sites retain their strength. If, however, an ensemble of cells is subject to sufficiently high tension or shear, some bonds will break and new ones may form. This occurs in particular during growth, when a duplicating cell needs to displace its neighbors to make room for its daughter cells. This qualitative description highlights the need for a quantitative description of interaction forces involving the extracellular matrix, including viscoplastic phenomena. A similar description is needed for the adhesions between cells, which provide a mechanism for the release of excessive stresses.
Another interesting mathematical problem is related to the fact that mechanical measurements are often done on single cells; for continuum mechanics, the information needs then to be upscaled from the microscopic to the macroscopic level.
Finally, invading cells pull on the extracellular matrix as they move through it. An understanding of this process requires evaluation of the adhesion forces and the mechanical forces that the cells are able to exert on the extracellular matrix. In his talk in Zurich during the embedded ESMTB meeting, Davide Ambrosi [1] presented a powerful method for obtaining this information from experimental data on substrate deformation, along with studies of the differences between normal and tumor cells.
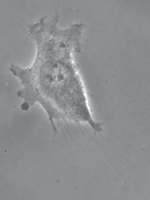
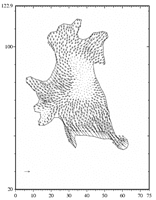
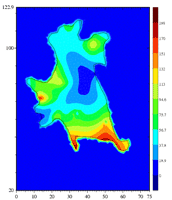
Tumor cell (T24) adhering to a polyacrylamide substrate. The displacement of the substrate at some points below and around the cell is known. These values are used to obtain the shear stress. The maximum calculated traction is about 200 piconewtons per square micrometer.
Where are we now?
From a theoretical viewpoint, all ingredients are ready for a merging of mechanical and chemical cues in a single mathematical model. Additional experiments are needed, however, to provide more robust foundations for mechano�chemical models and to validate the models.
Another more challenging, long-term research direction stems from the observation that in all the processes briefly described here, the mechanical behavior, either of an ensemble of cells or of a single cell, depends crucially on what happens inside the cells. One of the biggest mathematical challenge today is to describe the mechanical behavior of tissues not as a single-scale view but as a multiscale landscape.
This long-term project will require synergy among many researchers, the formation of multidisciplinary teams, and, of course, financial support. In this respect, the identification of cancer modeling as a key topic by some funding agencies---including the EU Commission, and the U.S. National Science Foundation and National Cancer Institute--has surely contributed to the surge of activity of the past decade; the large research networks formed, including that coordinated by the Politecnico di Torino (calvino.polito.it/~mcrtn) and the Center for the Development of a Virtual Tumor (www.cvit.org), provide vital support for research activities in this field.
References
[1] D. Ambrosi, Cellular traction as an inverse problem, SIAM J. Appl. Math., 66 (2006), 2049�2060.
[2] D. Ambrosi and L. Preziosi, On the closure of mass balance models for tumor growth, Math. Mod. Meth. Appl. Sci., 12 (2002), 737�754.
[3] M. Chaplain, L. Graziano, and L. Preziosi, Mathematical modelling of the loss of tissue compression responsiveness and its role in solid tumour development, Math. Med. Biol., 23 (2006), 197�229.
[4] J. Galle, M. Loeffler, and D. Drasdo, Modelling the effect of deregulated proliferation and apoptosis on the growth dynamics of epithelial cell populations in vitro, Biophys. J., 88 (2005), 62�75.
[5] M.J. Paszek, N. Zahir, K.R. Johnson, J.N. Lakins, G.I. Rozenberg, A. Gefen, C.A. Reinhart-King, S.S. Margulies, M. Dembo, D. Boettiger, D.A. Hammer, and V.M. Weaver, Tensional homeostasis and the malignant phenotype, Cancer Cell, 8 (2005), 241�254.
[6] L. Preziosi and A. Tosin, Multiphase modeling of tumor growth and extracellular matrix interaction: Mathematical tools and applications, J. Math. Biol. (2007), in press.
[7] B. Ribba, O. Saut, T. Colin, D. Bresch, E. Grenier, and J.-P. Boissel, A multiscale mathematical model of avascular tumor growth to investigate the therapeutic benefit of anti-invasive agents, J. Theor. Biol., 243 (2006), 532�541.
Luigi Preziosi is a professor of mathematics at Politecnico di Torino.

