How Geologists See Underground
December 17, 2007
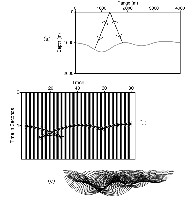
Reflection seismology. (a) A simple single-reflector model; (b) a synthetic seismogram. The radii of the circles in (c) are determined from the corresponding traces in (b). Figure adapted with permission from Norman Bleistein, "Hagedoorn Told Us How To Do Kirchhoff Migration and Inversion," The Leading Edge, Vol. 18, August 1999, pages 918�927.
The accompanying diagrams illustrate a simple example of reflection seismography. An exploration seismologist sets off explosions at constant intervals on Earth's surface. The explosions create seismic waves that propagate into the ground, bounce off a reflecting layer under the surface (a), and come back up, where they are recorded by a seismometer. In the simplest case, the seismometer is located at the place where the explosive charge was set off. In this case, the only waves the seismometer will "see" are the ones that hit the reflecting layer at a right angle. Any other wave would bounce off at an oblique angle and emerge somewhere else.
The seismographs, one for each charge, are turned vertically and placed side by side (b). It is easy to see in (b) that they form a shock wave, but its shape does not quite match the shape of the underground reflecting layer. Some of the vertical traces even show two or three shocks. That occurs because a shock wave might leave the source in two different directions, bounce perpendicularly off the reflecting layer in two different places, and then return to the original source location at two different times. (The seismograms record only the time of arrival, not the direction in which the wave was traveling.) To recover the shape of the reflecting layer, geologists draw (or used to draw) circles like the ones seen in (c)---each one with a radius determined by the corresponding trace in (b). The envelope of these circles---i.e., the heavy curve where they "accumulate"---reproduces the shape of the underground reflector. This procedure, invented by a Dutch seismologist, J.G. Hagedoorn, is called Kirchhoff migration.
Real life, of course, is not so simple. This example assumes quasi-homogeneous media above and below the reflector. It does not reveal anything about the speed of the seismic waves in the media, which gives geologists important information about the composition of the layers. It also fails to take into account that the interface between two rock layers is not like a perfect mirror; in practice, seismic waves can scatter in various directions. All of these issues can be handled by microlocal analysis. Oil and gas prospectors use a fairly tame version, in which the inversion procedure from seismograms to physical structure is well behaved. However, over the last twenty years, mathematicians, including Gregory Beylkin of the University of Colorado and Gunther Uhlmann of the University of Washington, have worked out general techniques, called Fourier integral operators, which apply in the deep Earth as well as close to the surface. "You can do things the practical seismologist was not aware of," says Maarten Van de Hoop.---DM

