Swarming: From Simple Models to Promising New Robotic Applications
November 14, 2009

Andrea Bertozzi of UCLA (left) gave the 2009 AWM�SIAM Sonia Kovalevsky Lecture, �Swarming by Nature and by Design,� in Denver at the SIAM Annual Meeting. Shown here with SIAM president Doug Arnold and AWM president Georgia Benkart, Bertozzi was cited by the award committee �for her mastery of an impressive variety of mathematical methods, ranging from partial differential equation estimates to numerical algorithms.� The award also recognized her �fundamental contributions� to fluid dynamics, nonlinear PDEs in image processing, and cooperative systems. In devoting the lecture to the latter, she pointed out, she was both honoring Sonia Kovalevsky, who worked in PDEs, and tailoring the talk to a meeting held in conjunction with the biennial conference of the SIAM Activity Group on Control and Systems Theory.
Michelle Sipics
On seeing a flock of birds or a school of fish, most people briefly acknowledge the wonders of nature, then move on. Few focus on an individual goose or herring, or wonder for more than a moment how it's interacting with its neighbors, or how the individuals are coordinating their movements to stay together.
That can be left to Andrea Bertozzi.
Bertozzi, the director of applied mathematics at the University of California, Los Angeles, gave the SIAM/AWM Sonia Kovalevsky Lecture at this year's SIAM Annual Meeting on one of her current interests: swarming. In the talk, titled "Swarming by Nature and by Design," Bertozzi covered efforts to introduce concepts of physics into mathematical biology models, develop and improve on continuous and discrete models of swarming, and advance potential applications of the work.
"First Principles" of Swarming
The basic properties of biological aggregations tend to be fairly simple, Bertozzi points out. A group executes a large-scale, coordinated movement, but without centralized control; the density of the group remains fairly constant toward the center and has a sharp edge at the aggregation's periphery; and the distance over which individuals can interact tends to be much smaller than the group's overall size. These properties allow for simple models under basic assumptions, like a conserved population and a velocity vector dependent on local population gradients.
Bertozzi and her colleagues are working to extend these simple models.
"If we see this in nature, we have to find models that have that behavior," she says. "But rather than using [global] behavior to construct the model, we want to think about constructing a model based on local interactions, and then see [if] that model yields the global behavior we're expecting."
Bertozzi and then-postdoc Chad Topaz demonstrated this approach in a 2004 paper in SIAM Journal on Applied Mathematics, modeling the propagation of constant-density groups in two dimensions. Although the model is limited in the kinds of behavior it can simulate, as Bertozzi explained in her talk, it does result in interesting patterns, such as rotation---similar to vortex motion for two-dimensional fluids. Moreover, the analogy between aggregation and fluids has led to some new mathematics. Recently, for example, Bertozzi and collaborators Thomas Laurent and Jos� Carrillo, as described this year in Nonlinearity, proved a sharp condition on the shape of the interaction kernel such that the basic aggregation model blows up in finite time.
From there, she moved on to new models, trying, as she puts it, to "think like a physicist" and identify "first principles" of swarming: for example, that the population of individuals in a swarm would sense the "average" density of the nearby population. Being biologically sensed, this average would decay over distance. In addition, because social attraction is the main precursor of swarming, members of the group would tend to climb population gradients---that is, move toward the areas where more individuals are gathered. This collection of "first principles" related to social attraction is what Bertozzi used to predict velocity in the new model.
Along with attraction, the models need a mechanism for dispersal. If overcrowding occurred without such a mechanism, the model would essentially be trying to place multiple individuals in the same physical space. Hence the first principles of dispersal: If members of the group get too close to each other, they should descend population gradients, and the strength of the dispersal should be proportional in some way to the amount of overcrowding---that is, the local density. (As Bertozzi explains, "If I'm not crowded in the first place, why would I want to bother [participating in] some kind of anti-crowding mechanism?")
The PDE model Bertozzi developed, with Topaz and Mark Lewis, yielded what she calls "beautiful clumping patterns." With a large population, the clumps tend to aggregate into a swarm with constant density and sharp edges---a result that also holds in two dimensions and reflects the swarms of locusts and schools of fish seen in nature. (The work appeared in the Bulletin of Mathematical Biology in 2006.)
Such models could be an important step toward harnessing the power of swarms for real-world applications in myriad fields. The applications in sensor networks alone are numerous, as artificial platforms can overcome some of the biological limitations of animal swarms. Take, for example, a school of fish.
"Unless there's some secret ESP we don't know about," Bertozzi says, fish probably don't communicate over very large distances. "But that doesn't mean that you couldn't accomplish that with an artificial network, using radio, or [another form] of communication."
A swarm of robots, then, might be used for remote sensing, with individual robots transmitting the information both to each other and, if needed, to a distant observer. Having multiple individuals take readings in the same area builds in redundancy, improving accuracy even if the sensor data is noisy; and the swarm, whatever it's measuring, could be sent into environments too dangerous for human beings.
"You might immediately think of defense," Bertozzi says, noting that her group is currently studying applications that involve searching for targets, including land mines. "But then you think of forest fires and so on, and there are so many basic problems that are very important for humanity."
Order in Chaos
To develop practical algorithms for real-world use, Bertozzi and her colleagues began developing discrete models that would track individual particles in a swarm.
The velocity of a particle in a swarm, Bertozzi explains, changes in response to multiple forces exerted on it: internal propulsion (for the purposes of a model, essentially a motor), friction, and forces produced by pairwise interactions between the particles, such as gravity. A model that adequately reflects real-world behavior must consider these forces.
One second-order model studied by Bertozzi and colleagues uses Rayleigh friction and Morse potential to model pairwise interactions. At that point, the question of the H-stability of the system arises.
A thermodynamic system in which the energy per particle scales with the system's size is called H-stable. By contrast, a system whose energy becomes infinite as the number of particles increases is H-unstable, or catastrophic. The Morse potential can be either H-stable or catastrophic, depending on system parameters: Very slight changes in parameters can result in large changes in behavior. With the H-unstable potential, the model leads to a very neat mill vortex that looks just like a school of fish, with all particles rotating at the same speed. With the H-stable potential, the swarmers move in a rigid-body rotation. Exactly why this occurs is not known, but Bertozzi and her group have demonstrated (in a 2006 paper published in Physical Review Letters) that the change in behavior is associated with the H-stability of the potential.
They also found that their dynamic continuum models can be valid for the catastrophic regime, but not for the H-stable case. Agreement between discrete and continuum models holds only in the catastrophic case, as Bertozzi explained in her talk.
"In the catastrophic case, the typical distance between particles is much smaller than the characteristic length scale associated with the potential," she said. "This means that you can approximate the discrete sum of pairwise interactions by a continuum integral of the potential. However, for H-stable swarms, the interparticle distance is comparable to the length scale of the potential---so the details of the shape of the potential are lost.
"The same issue arises in continuum limits of interacting molecules," she continued, describing work published in Physica D (2007). "For example, we do not describe a continuum fluid in terms of Lennard�Jones interactions between molecules."
Follow the Yellow Brick---or the Blue Tape---Road
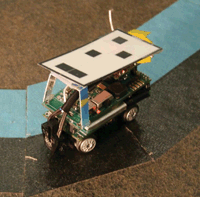
Autonomous robot designed and built by students in the applied math laboratory at UCLA. The robot carries a downward-looking infrared sensor that measures the color of the floor. An on-board processor running algorithms that determine the robot's path keeps it tracking the blue tape boundary, as shown here. A wireless antenna allows it to communicate with other robots and with a central computer.
Even with discrete models that more accurately capture real-world behavior, technical challenges must be addressed before such systems can be implemented. Longevity is an issue for devices being sent into hostile environments, as are energy consumption and reliable communications. Bertozzi has been involved with robotics experiments for the last five years, with the goal of testing various sensing and cooperative motion algorithms on laboratory testbeds. Her interest dates back to 2004, when she worked on a project involving Nekton Research (now part of iRobot) studying environmental boundary tracking. Soon afterward, Richard Murray of Caltech invited her to bring some UCLA students to his Multi-Vehicle Wireless Testbed to test algorithms.
"I found a club at UCLA where the students were building robots for a competition," Bertozzi remembers. "I got three outstanding students: Chung Hsieh, Bao Nguyen, and David Tung."
The students took advantage of Murray's offer, and eventually became co-authors (with Murray, Bertozzi, then-PhD student Zhipu Jin, and then-postdoc Daniel Mar-thaler) of two American Control Conference papers---on a testbed implementation of robots following an environmental boundary and an implementation of the Morse potential pairwise interaction model on a vehicle called the Kelley, which rolls on casters and uses model airplane fans for propulsion. Afterward, Hsieh decided to stay at UCLA in a master's degree program in engineering; with other students, he ended up designing robots for a testbed that Bertozzi and engineering colleague Emilio Frazzoli developed in the Applied Math Lab at UCLA.
The faculty researcher�undergrad collaboration has continued ever since; students in mathematics and engineering alike have contributed to the implementation of Bertozzi's algorithms.
"They come up with ideas and think that it's so much fun, and they can't believe someone's going to pay them to do this," Bertozzi says, recalling that electrical engineering undergraduate Kevin Leung designed a robot car from scratch with a $20 sensor after realizing he could improve on the first-generation testbed they had used. Of course, with new hardware, new algorithms were needed to govern their movement. Cue Vlad Voroninski, another undergraduate---this time in mathematics---who implemented a differential equation steering-control model, developed at the Naval Research Lab, on the testbed.
The UCLA testbed has since been used for many new projects, including a joint effort of UCLA and the Institute for Pure and Applied Mathematics on environmental mapping by robots with limited sensor data, as well as a biomimetic boundary-tracking project undertaken by Trevor Ashley, a Harvey Mudd undergraduate. Ashley, with Bertozzi and UCLA electrical engineering graduate students Abhijeet Joshi and Rick Huang, implemented an algorithm in a vehicle that tracks a boundary separating two regions based only on local sensor information, even with a low signal-to-noise ratio.
Using an on-board analog-to-digital converter, they applied a cumulative sum filter to the sensor data to determine whether a vehicle had crossed the boundary; the filtered data was then output to a steering controller that determined when course corrections were required to keep moving along the boundary. The algorithm and the motion of the robots call to mind an ant following a pheromone trail on the ground.
Cooperative sensing algorithms are already in use. Bertozzi mentions Naomi Leonard, an engineering professor at Princeton who has used small robot fleets to monitor algae blooms in Monterey Bay, California (see "Control Theorists Chart New Waters for Synchronized Swimmers," SIAM News, November 2005). Bertozzi and colleagues have extended the robot boundary-tracking algorithm, implementing it to find edges in high-dimensional hyperspectral imagery; she is currently working with researchers at Lawrence Berkeley National Laboratory to use these algorithms to control an atomic force microscope.
Other algorithms, designed to locate individual targets, are being implemented. "In looking at some of these applications in searching for targets, we're looking at how efficient it is to have a team. And if you have a team composed of swarms, is there an optimal swarm size?" Bertozzi asks. "We've found that there is---you actually do better with a small group working together than using the same resources and sending them out as individuals."
In other words, it's all about teamwork---whether you're a researcher or a robot.
Michelle Sipics is a contributing editor at SIAM News.

