Curing Ill Surfaces

April 6, 2011

Dana Mackenzie

In the last half-century, computers have dramatically affected the process used by engineers to determine whether their designs will work. Will this plane fly? Will that car protect us in a crash? At one time, such questions were answered with expensive prototypes. Now, more and more often, a differential equation solver provides the answers.

But the computer has also divided engineers into two tribes---designers and analysts---who use different kinds of software and speak different languages. The designers, for the most part, speak NURBS, a mathematical representation available in all computer-aided design software. NURBS (non-uniform rational B-splines) produce sleek, smooth curves and surfaces that look great on a drawing board or computer screen. The analysts decompose these elegant but often deceptive pictures into finite-element meshes, which are traditionally considered superior to splines for figuring out how bumpers will crumple or wings will vibrate.

"Finite-element analysis and CAD are both billion-dollar industries, with a very fragile baton-passing interface," says Tom Hughes, who holds a chair in computational and applied mathematics and is a professor of aeronautical engineering at the University of Texas. "They don't really interact in their core." According to a 1999 study by the National Institute of Standards and Technology, the bottleneck between CAD and analysis was costing the U.S. automotive industry alone more than $600 million per year.

Hughes is in the forefront of a small but growing movement to unify engineering design and analysis by developing design tools that can be plugged straight into analysis programs. Six years ago, he coined the name "isogeometric analysis" for the fledgling discipline.

In January 2011, the first conference on isogeometric analysis, organized by Hughes, along with Dave Benson and Yuri Bazilevs of the University of California, San Diego, showed how fast the new subject has grown. More than a hundred people traveled to Austin, Texas, for the workshop, more than 60 of them from outside the United States. Hughes had expected to schedule 36 talks, but there were so many submissions that he had to reserve a second conference room and double the number of talks.

"I think this will be a landmark conference for kicking off the whole movement," says Rich Riesenfeld of the University of Utah, an early pioneer in B-spline curves and surfaces. "We'll look back five years from now and say this event in Austin was where everything started."

For the time being, the conference show-ed that isogeometric analysis offers more questions than answers. But it is already providing ideas for new start-ups and giving researchers in CAD and finite elements a new focus. "It's a new challenge after ten quiet years," says Tor Dokken, a CAD researcher at SINTEF, an independent research lab in Norway.

Tugging on Superman's Cape
Tom Sederberg, a computer scientist at Brigham Young University, likes to illustrate the difference between design and analysis with a teapot. In the world of computer graphics, the "Utah teapot," first rendered on a computer screen by Martin Newell of the University of Utah in 1975, has become both a standard image and an in-joke. It has four pieces: a bowl, a spout, a handle, and a lid. They were rendered with bicubic splines, a simple and popular version of NURBS.

Each piece was trimmed to fit the adjoining pieces. When you put them all together on the computer screen, you see what appears to be a perfect fit. But if you were to add computer-simulated water, you would find that the teapot leaks (see Figure 1). In fact, it can be proved mathematically that it must leak! The surfaces are defined by polynomials of degree 18, whose intersection is a curve of degree 324--a curve that cannot be modeled exactly by cubic splines.

As whimsical as the example seems, the Utah teapot is exactly the sort of model that designers hand over to analysts all the time. Imagine trying to analyze an airplane wing that isn't completely attached to the airplane. It's no wonder that analysts, confronted with ailing surfaces like these, want to replace them with something more robust and airtight. That "something" is a finite-element model.

The classic finite-element method takes a connect-the-dots approach to describing a curve, a surface, or a volume. The vertices of a finite-element mesh lie directly on the surface to be modeled. Between vertices, the model has facets defined by low-order polynomials, usually linear; it is therefore not smooth, and it does not exactly match the physical surface, the airplane wing or the car body.

A NURBS patch, by contrast, can be visualized as a smooth rectangular piece of fabric, patched together from a set of smaller rectangular pieces, the whole levitated in midair like Superman's cape. The shape of the cape is adjusted by a set of "control points," located at the intersections of an invisible net. Neither the net nor the control points need to lie on the surface; they merely hover near it. A tug on one control point affects the part of the cape closest to it. (Typically, each control point affects a 4-by-4 square of surface elements, so that the domain of influence of neighboring control points overlaps slightly. This overlap allows for a smooth transfer of power from one control point to the next.) See Figure 2.


Figure 2. A NURBS "control net" hovers over a physical surface. Red dots represent control points; rectangles with red dots at the corners represent parts of the net. The physical surface is defined by smooth "basis functions" that interpolate between the locations of the control points. The blue rectangle is one "finite element" on the physical surface. The six finite elements seen here intersect smoothly along their boundaries. Courtesy of Dave Benson.

Both finite elements and NURBS have advantages and drawbacks. Despite the importance of smoothness in aerodynamics and a number of other applications, classic finite-element meshes are not smooth. And, as Hughes has shown, more subtle problems occur in the analysis of vibrations: The edges between facets of the mesh act like hinges, allowing tiny, physically unrealistic vibrations to occur.

NURBS, for their part, are smooth within patches and faithfully reflect the shape intended by the designer. But they are limited in topology; they can be used only to describe surfaces that can be covered by a rectangular net. For a complex surface like a teapot or a car, you may have to trim pieces from a patch or sew patches together---and that's when the mischief begins. (Remember the Utah teapot.) If you sew two "Superman capes" together, without carefully matching the size of the patches, the resulting cape will have T-junctions. Likewise, removal of part of a seam from the cape will produce T-junctions. In NURBS, these are not allowed.

Moreover, NURBS surfaces have issues of refinability. You can't make a rectangular net finer locally; if you want to improve the resolution of your surface in one area (near a rivet, say), you can't just add a control point---you have to add an entire new row or column.

Perhaps the worst problem, though, is not inherent to either method alone: It is the huge number of hours wasted on translating NURBS surfaces into finite-element meshes. Hughes estimates that more than 80% of the time nominally spent on analysis is actually spent on this drudgery. His graduate student Ben Urick, formerly a structural engineer for an architectural firm, places the figure even higher. "Ninety percent of my time as a design engineer was spent in pre-processing and analysis," he says; the time left for actual decision-making was inadequate. "In the end, I would say that parts of designs succumbed to conservatism because of this process, which defeats the purpose of making complex computational models."

Around 2003, Hughes, with then graduate students Yuri Bazilevs and Austin Cottrell, started to play around with the idea of using NURBS instead of finite elements to solve differential equations. Thus was born the isogeometric mandate: to use the same "basis functions" for design and analysis. (NURBS weren't the only option, but Hughes chose them because they were standard in the engineering CAD industry.) "We found that things weren't just working better, but way better," Hughes says. After the encouraging simulations, Bazilevs says, "It was clear in my mind that the next thing to do was a rigorous mathematical theory."

Bazilevs and the rest of the team showed that NURBS-based finite elements perform just as well as classic finite elements for simple equations, such as Poisson's equation. But, Bazilevs points out, "Where isogeometric analysis really shines is where you need extra continuity"---that is, for basis functions with one or more derivatives. The Kirchhoff�Love equation for the bending of a thin shell, for example, involves fourth derivatives, and even a weak solution must have continuous first derivatives. A classic finite-element model simply won't work.

The suitability of NURBS for analysis was thus well established by 2005. In fact, experts in B-splines had long suspected that this would be the case. "We just needed a well-known, high-powered guy from finite elements to say that these were good for analysis and promote the idea," says Elaine Cohen of the University of Utah. That guy was Tom Hughes, who describes himself as a "pied piper" linking the two fields.

T-Splines and 3-D Meshes
The focus at the Austin conference was on the unfinished parts of the isogeometric agenda: specifically, on the problems of T-junctions and refinability, and of representing three-dimensional volumes. The meeting also featured many new applications, from biomedical engineering to fluid�structure interactions to electromagnetic fields.

The issues of refining, trimming, and sewing patches together seem to be near solution, thanks to Sederberg's invention in 2003 of T-splines. As the name suggests, these are spline functions that can be defined on any mesh of quadrilaterals, even those with T-junctions. Though conceived independently, T-splines and isogeometric analysis seem to be built for one another. T-splines hit a bump in 2009, with the discovery that the meshes cannot be completely arbitrary: In certain rare cases the splines are linearly dependent, which means that the differential equation solver can blow up. After several months of hard work, however, Sederberg's group identified a very mild restriction on T-meshes that guarantees "analysis-suitable" splines. (See Figure 3.)


Figure 3. Sederberg's solution to a problem that threatened to scare off possible users of T-splines. Beginning at each T-inter-section (blue points), draw a yellow line segment "two bays out and one bay back." If none of the yellow line segments intersect, then the T-spline mesh is "analysis-suitable." This means that the basis functions used to draw the surface can also be used to solve the differential equations describing its physical properties. Courtesy of Tom Sederberg.

Meanwhile, T-splines are moving rapidly toward practical implementation. Sederberg co-founded T-Splines Inc., which has developed a T-spline plug-in for a widely used open-source CAD program called Rhinoceros. SolidWorks, a major commercial CAD vendor, announced a week after the conference that it will also integrate T-splines into its software.

On the application side, analysts are taking on more challenging and realistic problems. An example is work on wind turbines presented by Bazilevs at the conference. The turbine blades are described by the Kirchhoff�Love equations, while the air obeys the Navier�Stokes equations for fluids. These sets of equations, each hard to solve in isolation, are coupled in a wind turbine, with the turbine blade acting as a moving boundary for the fluid problem. The turbine blades could be modeled with T-splines, but to solve the fluid�structure interaction Bazilevs needed a compatible mesh for the volume between the turbine blades (Figure 4).


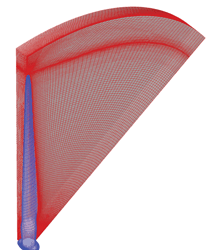
Figure 4. A NURBS parametrization of the region between turbine blades, visualized as a distorted 60� slice of pie. The mesh has been made finer in the regions where the most turbulence is expected to occur. A finer mesh allows for a more accurate solution of the fluid flow equations in those regions. Courtesy of Yuri Bazilevs.

Three-dimensional modeling is still a notoriously difficult challenge for NURBS.Bazilevs visualized the region between the blades as a distorted 60� slice of pie. He easily found a suitable mesh for this "template" region, to which he added enough control points to distort the mesh into a form that would fill the region between blades. Bazilevs believes that this three-step procedure---find a template mesh, refine it, and then distort it to fit the desired region---could be used for many practical problems that require a NURBS volume mesh. Using the method, he figured out how to pre-bend the turbine blades so that they would straighten out when the rotor is spinning. His answer specifies blades that look very similar to those of a turbine that is on the market (and that presumably was designed by trial and error).

For now, it is an open question when and whether isogeometric methods will make their way into the marketplace of CAD and finite-element software. "They're big industries and they are not going to change overnight," Cohen says.

"In the commercial sector there's the need to validate the software, and it will take time to pass standards," says Bob Taylor, a retired professor of engineering at the University of California at Berkeley and a longtime expert on finite elements. He now works part time for a company called Simulia, which does not currently offer isogeometric analysis in its products---a fact that Taylor attributes in part to the economy.

"The areas I see it moving into are, first of all, sheet forming," Taylor says. Stamped metal sheets, like those in the body of a car, can often be treated as two-dimensional surfaces, with no need for volumetric parametrizations. Because surface-based equations involve higher derivatives, sheet forming plays to the strengths of isogeometric analysis. Another area on which Taylor expects isogeometric analysis to have an impact is the modeling of surfaces that have to slide against each other. Faceted meshes catch against each other, whereas smooth NURBS surfaces can glide freely.

For complicated three-dimensional objects, such as an engine block, or applications for which smoothness is a low priority, isogeometric analysis is less likely to catch on soon. And while isogeometric analysis moves forward, its competition---including methods for automating the translation from NURBS to finite elements---is not standing still. "It isn't as much of a bottleneck as it used to be," says Mark Beall, the president of Simmetrix, which makes mesh-generation software. "Generating a few-million-element mesh is now a five minute wait." (Hughes considers this true only in ideal situations that are seldom encountered in industry.)

But the originator of the field is undaunted by the challenges. "I think that what we have here is a compelling, high-end problem with a compelling, high-end strategy that filters down into what everybody does," Hughes says. "I would be disappointed if it took more than five years for someone to make big noise in the analysis industry with this."

"I think we're on the right track," he adds. "Everybody that gets into this field winds up doing something interesting, and doing it much better than ever before. This is one of those areas that is just pregnant with possibilities."


Dana Mackenzie writes from Santa Cruz, California.

• See more news from this issue