The Mathematics of Face Recognition
April 30, 2003On March 10 The New York Times reported that an Internet security consultant, doubting that the "disheveled, dazed-looking man" arrested as Khalid Shaikh Mohammed was the man shown on the FBI's most-wanted posters, fired off messages to producers of face recognition systems, asking them to compare the arrest and poster images. The Canadian company AcSys Biometrics soon replied that the FBI had the right man. Wondering about the mathematics of the systems used by companies like AcSys, SIAM News got in touch with David Wilson, program director of SIAM's activity group in imaging. Wilson, in turn, sent out e-mail queries, which drew a flurry of responses pointing to research groups working on the (still challenging) problem of face recognition, along with the brief overview of the field that follows, by Ron Kimmel of the Technion and Guillermo Sapiro of the University of Minnesota.
Ron Kimmel and Guillermo Sapiro
Face recognition, the art of matching a given face to a database of faces, is a nonintrusive biometric method that dates back to the 1960s. In efforts going back to far earlier times, people have tried to understand which facial features help us perform simple recognition tasks, such as identifying a person, deciding on an individual's age and gender, and classifying facial expression and even beauty. We are puzzled by the smile of DaVinci's Mona Lisa, for example-what is it that makes it so special? Research in this area has intrigued psychologists, behavioral scientists, artists, and, more recently, mathematicians and engineers. In this note we describe some of the underlying mathematical tools used in state-of-the-art face recognition computer systems.
Why is computer-based face recognition challenging? To begin with, a recognition system has to be invariant both to external changes, like environmental light, and the person's position and distance from the camera, and internal deformations, like facial expression, aging, and makeup. Because most commercial applications use large databases of faces, recognition systems have to be computationally efficient. Given all these requirements, mathematical modeling is not so simple. It is clear that we are not working under simple invariant theory, such as Lie group invariants, and that different tools are needed. In the next few paragraphs we describe some of the basic underlying principles now being used to address these invariant pattern recognition tasks.
Most face recognition algorithms fall into one of two main groups: feature-based and image-based algorithms. Feature-based methods explore a set of geometric features, such as the distance between the eyes or the size of the eyes, and use these measures to represent the given face. These features are computed using simple correlation filters with expected templates. These methods are somewhat invariant to changes in illumination and can partially compensate for changes in camera location. However, they are sensitive to aging and facial expressions. It is also not clear which features are important for classification, an area in which more mathematical studies are needed. There are fundamental mathematical results in the literature that try to address these questions and have not yet been fully exploited for face recognition. Actually, the first documented work on computerized face recognition---by Bledsoe, more than 40 years ago---was based on exactly these ideas. Image-based systems, the other main approach to face recognition, are based on ideas like eigenfaces (see Figure 1). After a large training set of images has been collected, principal component analysis is used to compute eigenfaces. Each new face is then characterized by its projection onto this space of principal eigenfaces. This approach is extremely sensitive to small variations, both external and internal, though it is still one of the most popular methods in industry. Leading research in this area was conducted by Turk and Pentland (and by their contemporaries Kirby and Sirovich).


Figure 1. The eigenface approach. Sample training faces are shown (left), followed by the first 15 principal eigenfaces. A 2D face is represented by its projection onto this space. (Data from http://www.geop.ubc.ca/CDSST/eigenfaces.html.)
Most current commercial systems still deal with "flat" images, from which they extract features or eigenfaces. Cheap commercial cameras capture two-dimensional images in which the geometry of the face is represented mainly through its light-reflection properties. It is possible to imagine cameras that capture the facial surface embedded in three-dimensional space. It was, in fact, in testing results of face recognition systems based on two-dimensional flat images that scientists were motivated to explore the geometric properties provided by three-dimensional systems.
The first task is to get a 3D model of the face. Approaches include use of more than one camera, also known as "shape from stereo," and "structured light," i.e., projecting a known pattern on the face and performing simple triangulation techniques. A number of universities and companies have developed systems for real-time 3D acquisition based on these ideas. These systems are still relatively expensive, however, and have not been fully developed to work efficiently at high resolution or at large distances from the subject. Once the 3D model is obtained, invariant measures can be extracted.
In work done at the Technion, for example, the first author's group (see Figures 2 and 3) first computes geodesic distances between sampled points on the facial surface. Based on these distances, the points are then flattened into a low-dimensional Euclidean space, providing a bending invariant (or isometric invariant) signature surface that is robust to certain facial expressions. Finally, the signature is compared with a database of signatures. Three-dimensional systems are intrinsically position- and light-invariant, and when computed as described here, can also be invariant to some facial expressions. Three-dimensional systems can obtain results not possible with 2D systems, such as distinguishing between identical twins under various facial expressions (Figures 2 and 3).

Figure 2. Three-dimensional face recognition with isometric signatures. Two-dimensional pictures of the subjects are shown in the first row; the second row depicts the 3D facial surfaces acquired by a range camera (structured light), and the third row shows the canonical isometric signatures (projections based on geodesic distances). Distances of the subjects from the reference subject (Alex 0) were computed, using a surface matching (first row of numbers) and isometric signature matching (second row of numbers). Notice the small inter-instance distances and the large distance from the control subject (Oscar 0) when invariant signatures are used. (Courtesy of A. Bronstein, M. Bronstein, and R. Kimmel, 2003.)
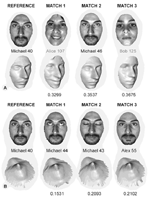
Figure 3. Three-dimensional face recognition with isometric signatures. The first row shows 2D pictures of the subjects, the second row 3D facial surfaces acquired by a range camera. Search for the closest matches in the database to subject 40 (Michael) was done by matching of facial surfaces (A) and by isometric signatures (B). The distances to the reference subject (first column) are shown in the bottom rows of A and B. (Courtesy of A. Bronstein, M. Bronstein, and R. Kimmel, 2003.)
As one of the most important biometric methods, face recognition has been an area of intense research. An Internet search on the key words "face recognition" returns tens of thousands of hits. Federal agencies in the U.S. have launched major funding initiatives (e.g., the HumanID effort at DARPA).
Are we already at the stage of fully automatic face recognition systems like those we see in science fiction movies? The answer is probably no, although we're getting there. For tasks like searching for faces in complex scenes, a problem known as face detection, efficient and accurate solutions have been reported by groups using learning techniques, such as those introduced by Perona, Amit, Geman, Elad, Hel-Or, and Teo, or neural-network approaches like that developed at Carnegie Mellon University. A good nonintrusive recognition system would probably combine face recognition with other biometrics, such as gait, and skin or hair color; intrusive metrics, such as fingerprints and DNA, could be added for some applications. Integrated biosignatures constitute a very active research area, one that involves classic and modern mathematical tools, such as dynamical systems, geometric analysis of high-dimensional manifolds, and statistical learning. Progress in any of these areas should accelerate developments in this field.

